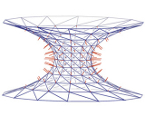
This catenoid is a complete discrete minimal surface whose vertices are given by explicit formulas.

This surface belongs to a 4-parameter family of complete discrete catenoids from which a 2-parameter subfamily interpolates the smooth catenoid. The discrete catenoids are the first explicitly known discrete versions of a complete minimal surface beside the trivial plane which are critical points of the variational problem for minimizing the discrete surface area. This explicit representation allows to generate exact discrete minimal surfaces without numerical errors which is useful, for example, in stability investigations.

The discrete H-T surface is a triply periodic minimal surface solving a free boundary value problem for the surface area. This example is of high numerical precision, and including its parametrization it was automatically computed by minimizing the alignment energy of a non-conforming conjugate minimal surface.

Minimizing the alignment energy in the space of non-conforming meshes enables us to produce discrete conforming minimal surfaces of a high numerical precision. The computed discrete H-T surface is a non-trivial example in the sense that it includes a branch point which is not induced from symmetry properties.

This discrete version of Schwarz' P-surface is a critical point of the area functional in the space of non-conforming meshes solving a free boundary problem.

Non-conforming meshes are a superset of the class of conforming meshes which appear as natural completion in the study of discrete constant mean curvature surfaces. For example, there exists a 1-1 pairing of discrete conforming and discrete non-conforming minimal surfaces.

Penta is a compact H-surface of genus 5 with pentagonal symmetry and is the first compact H-surface of genus > 1 which is successfully computed with a computer. The surface is defined via the conjugate surface construction by a two-parameter problem of minimal surfaces in S³. Numerical existence was shown by computing a sequence of H-surfaces with the algorithm of Oberknapp/Polthier and using a winding number argument. Further details on the Penta surface and its cousin are given in the article section.

Blaine Lawson found in 1970 a method to solve free boundary value problems for unstable Euclidean constant mean curvature surfaces by solving a corresponding Plateau problem for minimal surfaces in S³. Numerical simulations of this construction using standard numerical methods have failed up to now. The authors have found a numerical algorithm for this so-called "Conjugate Surface Construction for H-surfaces" based on the concept of discrete constant mean curvature surfaces. For the first time it allows computation and numerical experiments of a large set of H-surfaces, see e.g. the Penta surface in this image collection. The algorithm is implemented in the mathematical visualization software Grape.

The front object in the current picture shows a compact minimal surface of Lawson in S³ after stereographic projection from S³ to R³ (it looks smooth but the surface is 'discrete' at a fine level) and the object in the background is its conjugate surface, a periodic H=1 surface in R³.

The Quadend surface is a candidate for a family of a periodic minimal surfaces, where the genus of the fundamental building block can be made arbitrarily large. It is not yet completely proved but it is likely that the period problem can be made independent of the genus.

This surface belongs to a collection of new minimal surfaces in hyperbolic 3-space which I constructed in my thesis. These surfaces are solutions to a general Plateau Problem in H³ where parts of the boundary may lie in infinity and some other parts in the finite space.

The hyperbolic Scherk surface is an example which generalizes in some sense the Euclidean minimal Scherk surface which is given as a minimal graph over the white fields of a checker board. Here a major difference between minimal surfaces in Euclidean and hyperbolic space can be seen: the Euclidean surface is isolated with respect to its flat ends but the hyperbolic Scherk surface belongs to a family whose fundamental domains have the same finite boundary but different infinite boundaries. With other words, the conformal structure has much more freedom for a given finite part of a Plateau Problem.