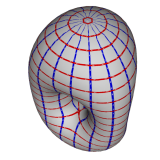
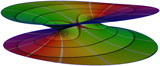
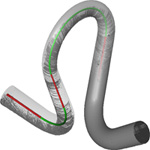
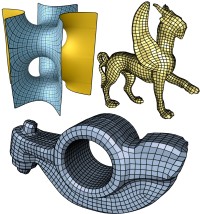
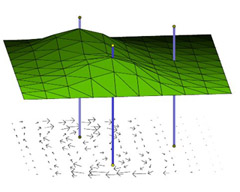
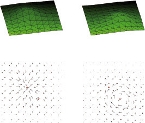
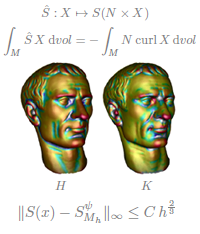Creating motions of objects or characters that are physically plausible and follow an animator's intent is a key task in computer animation. The spacetime constraints paradigm is a valuable approach to this problem, but it suffers from high computational costs. Based on spacetime constraints, we propose a framework for controlling the motion of deformable objects that offers interactive response times. This is achieved by a model reduction of the underlying variational problem, which combines dimension reduction, multipoint linearization, and decoupling of ODEs. After a preprocess, the cost for creating or editing a motion is reduced to solving a number of one-dimensional spacetime problems, whose solutions are the wiggly splines introduced by Kass and Anderson [2008]. We achieve interactive response times through a new fast and robust numerical scheme for solving the one-dimensional problems that is based on a closed-form representation of the wiggly splines.
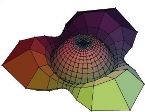
We present a new method for modeling discrete constant mean curvature (CMC) surfaces, which arise frequently in nature and are highly demanded in architecture and other engineering applications. Our method is based on a novel use of the CVT (centroidal Voronoi tessellation) optimization framework. We devise a CVT-CMC energy function defined as a combination of an extended CVT energy and a volume functional. We show that minimizing the CVT-CMC energy is asymptotically equivalent to minimizing mesh surface area with a fixed volume, thus defining a discrete CMC surface. The CVT term in the energy function ensures high mesh quality throughout the evolution of a CMC surface in an interactive design process for form finding. Our method is capable of modeling CMC surfaces with fixed or free boundaries and is robust with respect to input mesh quality and topology changes. Experiments show that the new method generates discrete CMC surfaces of improved mesh quality over existing methods
Presented at SIGGRAPH 2012
DOI:10.1145/2019627.2019638 (BibTex).
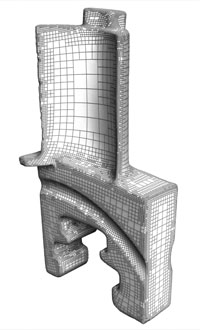
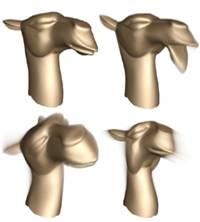
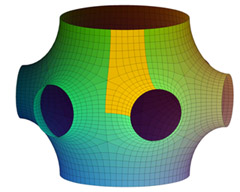
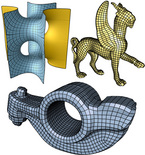
We propose a framework for deformation-based surface modeling that is interactive, robust and intuitive to use. The deformations are described by a non-linear optimization problem that models static states of elastic shapes under external forces which implement the user input. Interactive response is achieved by a combination of model reduction, a robust energy approximation, and an efficient quasi-Newton solver. Motivated by the observation that a typical modeling session requires only a fraction of the full shape space of the underlying model, we use second and third derivatives of a deformation energy to construct a low-dimensional shape space that forms the feasible set for the optimization. Based on mesh coarsening, we propose an energy approximation scheme with adjustable approximation quality. The quasi-Newton solver guarantees superlinear convergence without the need of costly Hessian evaluations during modeling. We demonstrate the effectiveness of the approach on different examples including the test suite introduced in [Botsch and Sorkine 2008].
DOI:10.1016/j.cagd.2012.01.001 (BibTex).
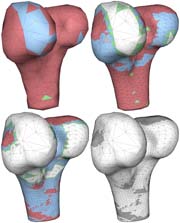
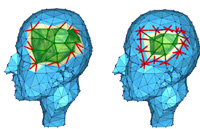
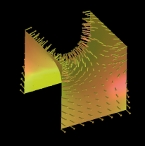
In recent years, substantial progress in shape analysis has been achieved through methods that use the spectra and eigenfunctions of discrete Laplace operators. In this work, we study spectra and eigenfunctions of discrete differential operators that can serve as an alternative to the discrete Laplacians for applications in shape analysis. We construct such operators as the Hessians of surface energies, which operate on a function space on the surface, or of deformation energies, which operate on a shape space. In particular, we design a quadratic energy such that, on the one hand, its Hessian equals the Laplace operator if the surface is a part of the Euclidean plane, and, on the other hand, the Hessian eigenfunctions are sensitive to the extrinsic curvature (e.g. sharp bends) on curved surfaces. Furthermore, we consider eigenvibrations induced by deformation energies, and we derive a closed form representation for the Hessian (at the rest state of the energy) for a general class of deformation energies. Based on these spectra and eigenmodes, we derive two shape signatures. One that measures the similarity of points on a surface, and another that can be used to identify features of surfaces.
We present a discretization of Koiter's model of elastic thin shells based on a finite element that employs limit surfaces of Catmull-Clark's subdivision scheme. The discretization can directly be applied to control grids of Catmull-Clark subdivision surfaces, and, therefore, integrates modeling of Catmull-Clark subdivision surfaces with analysis and optimization of elastic thin shells. To test the discretization, we apply it to standard examples for physical simulation of thin shells and compute free vibration modes of thin shells. Furthermore, we use the discrete shell model to set up a deformation-based modeling system for Catmull-Clark subdivision surfaces. This system integrates modeling of subdivision surfaces with deformation-based modeling and allows to switch back and forth between the two different approaches to modeling.
This work concerns the approximation of the shape operator of smooth surfaces in R3 from polyhedral surfaces. We introduce two generalized shape operators that are vector-valued linear functionals on a Sobolev space of vector fields and can be rigorously defined on smooth and on polyhedral surfaces. We consider polyhedral surfaces that approximate smooth surfaces and prove two types of approximation estimates: one concerning the approximation of the generalized shape operators in the operator norm and one concerning the pointwise approximation of the (classic) shape operator, including mean and Gaussian curvature, principal curvatures, and principal curvature directions. The estimates are confirmed by numerical experiments.
- Best Paper Award -
Discrete Laplace--Beltrami operators on polyhedral surfaces play an important role for various applications in geometry processing and related areas like physical simulation or computer graphics. While discretizations of the weak Laplace--Beltrami operator are well-studied, less is known about the strong form. We present a principle for constructing strongly consistent discrete Laplace--Beltrami operators based on the cotan weights. The consistency order we obtain, improves previous results reported for the mesh Laplacian.Furthermore, we prove consistency of the discrete Willmore energies corresponding to the discrete Laplace--Beltrami operators.
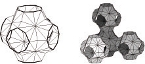
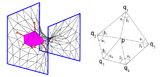
Despite the success of quad-based 2D surface parameterization methods, effective parameterization algorithms for 3D volumes with cubes, i.e. hexahedral elements, are still missing. CubeCover is a first approach for generating a hexahedral tessellation of a given volume with boundary aligned cubes which are guided by a frame field.
The input of CubeCover is a tetrahedral volume mesh. First, a frame field is designed with manual input from the designer. It guides the interior and boundary layout of the parameterization. Then, the parameterization and the hexahedral mesh are computed so as to align with the given frame field.
CubeCover has similarities to the QuadCover algorithm and extends it from 2D surfaces to 3D volumes. The paper also provides theoretical results for 3D hexahedral parameterizations and analyses topological properties of the appropriate function space.
Multiresolution meshes provide an efficient and structured representation of geometric objects. To increase the mesh resolution only at vital parts of the object, adaptive refinement is widely used. We propose a lossless compression scheme for these adaptive structures that exploits the parent-child relationships inherent to the mesh hierarchy. We use the rules that correspond to the adaptive refinement scheme and store bits only where some freedom of choice is left, leading to compact codes that are free of redundancy. Moreover, we extend the coder to sequences of meshes with varying refinement. The connectivity compression ratio of our method exceeds that of state-of-the-art coders by a factor of 2 to 7. For efficient compression of vertex positions we adapt popular wavelet-based coding schemes to the adaptive triangular and quadrangular cases to demonstrate the compatibility with our method. Akin to state-of-the-art coders, we use a zerotree to encode the resulting coefficients. Using improved context modeling we enhanced the zerotree compression, cutting the overall geometry data rate by 7% below those of the successful Progressive Geometry Compression. More importantly, by exploiting the existing refinement structure we achieve compression factors that are 4 times greater than those of coders which can handle irregular meshes.
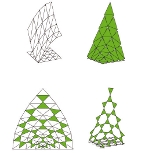
In this paper we introduce hexagonal global parameterizations, a new type of parameterization in which parameter lines respect six-fold rotational symmetries (6-RoSy). Such parameterizations enable the tiling of surfaces with regular hexagonal texture and geometry patterns and can be used to generate high-quality triangular remeshing.
To construct a hexagonal parameterization given a surface, we provide an automatic technique to generate a 6-RoSy field that respects directional and singularity features in the surface. We also introduce a technique for automatically merging and cancelling singularities. This field will then be used to generate a hexagonal global parameterization by adapting the framework of QuadCover parameterization.
We demonstrate the usefulness of our geometry-aware global parameterization with applications such as surface tiling with regular textures and geometry patterns and triangular remeshing.
Riemann surfaces naturally appear in the analysis of complex functions that are branched over the complex plane. However, they usually possess a complicated topology and are thus hard to understand. We present an algorithm for constructing Riemann surfaces as meshes in R^3 from explicitly given branch points with corresponding branch indices. The constructed surfaces cover the complex plane by the canonical projection onto R^2 and can therefore be considered as multivalued graphs over the plane – hence they provide a comprehensible visualization of the topological structure. Complex functions are elegantly visualized using domain coloring on a subset of C. By applying domain coloring to the automatically constructed Riemann surface models, we generalize this approach to deal with functions which cannot be entirely visualized in the complex plane.
In this work, we study the spectra and eigenmodes of the Hessian of various discrete surface energies and discuss applications to shape analysis. In particular, we consider a physical model that describes the vibration modes and frequencies of a surface through the eigenfunctions and eigenvalues of the Hessian of a deformation energy, and we derive a closed form representation for the Hessian (at the rest state of the energy) for a general class of deformation energies. Furthermore, we design a quadratic energy, such that the eigenmodes of the Hessian of this energy are sensitive to the extrinsic curvature of the surface.
Based on these spectra and eigenmodes, we derive two shape signatures. One that measures the similarity of points on a surface, and another that can be used to identify features of the surface. In addition, we discuss a spectral quadrangulation scheme for surfaces.
We study discrete curvatures computed from nets of curvature lines on a given smooth surface and prove their uniform convergence to smooth principal curvatures. We provide explicit error bounds, with constants depending only on properties of the smooth limit surface and the shape regularity of the discrete net.
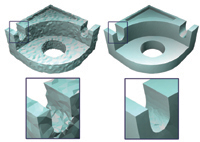
Structuring of surface meshes is a labor intensive task in reverse engineering. For example in CAD, scanned triangle meshes must be divided into characteristic/uniform patches to enable conversion into high-level spline surfaces. Typical industrial techniques, like rolling ball blends, are very labor intensive. We provide a novel, robust and quick algorithm for the automatic generation of a patch layout based on a topology consistent feature graph. The graph separates the surface along feature lines into functional and geometric building blocks. Our algorithm then thickens thickens the edges of the feature graph and forms new regions with low varying curvature. Further these new regions - so called llets and node patches - will have highly smooth boundary curves making it an ideal preprocessor for a subsequent spline tting algorithm.
We present a novel coder for lossless compression of adaptive multiresolution meshes that exploits their special hierarchical structure. The heart of our method is a new progressive connectivity coder that can be combined with leading geometry encoding techniques. The compressor uses the parent/child relationships inherent to the hierarchical mesh. We use the rules that accord to the refinement scheme and store bits only where it leaves freedom of choice, leading to compact codes that are free of redundancy. To illustrate our scheme we chose the widespread red-green refinement, but the underlying concepts can be directly transferred to other adaptive refinement schemes as well. The compression ratio of our method exceeds that of state-of-the-art coders by a factor of 2 to 3 on most of our benchmark models.
Classical surface parameterization algorithms often place singularities in order to enhance the quality of the resulting parameter map. Unfortunately, singularities of positive integral index (as the north pole of a sphere) were not handled since they cannot be described with piecewise linear parameter functions on a triangle mesh. Preprocessing is needed to adapt the mesh connectivity. We present an extension to the QuadCover parameterization algorithm, which allows to handle those singularities.
A singularity of positive integral index can be resolved using bilinear parameter functions on quadrilateral elements. This generalization of piecewise linear functions for quadrilaterals enriches the space of parameterizations. The resulting parameter map can be visualized by textures using a rendering system which supports quadrilateral elements, or it can be used for remeshing into a pure quad mesh.
We present a novel algorithm for automatic parameterization of tube-like surfaces of arbitrary genus such as the surfaces of knots, trees, blood vessels, neurons, or any tubular graph with a globally consistent stripe texture. We use the principal curvature frame field of the underlying tube-like surface to guide the creation of a global, topologically consistent stripe parameterization of the surface. Our algorithm extends the QuadCover algorithm and is based, first, on the use of so-called projective vector fields instead of frame fields, and second, on different types of branch points. That does not only simplify the mathematical theory, but also reduces computation time by the decomposition of the underlying stiffness matrices.
Die euklidische Geometrie von Eiflächen und Eikörpern bietet eine gute Gelegenheit, mathematischen Laien geometrische Begriffsbildungen und Sachverhalte aus der Flächentheorie plausibel zu machen. In dieser Arbeit erörtern wir die erstaunliche Stabilität von Eierschalen und dazu verwandte Probleme unter heuristisch-mathematischen Gesichtspunkten.
Complex-valued functions are fundamental objects in complex analysis, algebra, differential geometry and in many other areas such as numerical mathematics and physics. Visualizing complex functions is a non-trivial task since maps between two-dimensional spaces are involved whose graph would be an unhandy submanifold in four-dimensional space. The present paper improves the technique of “domain coloring” in several aspects: First, we lift domain coloring from the complex plane to branched Riemann surfaces, which are essentially the correct domain for most complex functions. Second, we extend domain coloring to the visualization of general 2-valued maps on surfaces. As an application of such general maps we visualize the Gauss map of surfaces as domain colored plots and establish a link to current surface parametrization techniques and texture maps. Third, we adjust the color pattern in domain and in image space to produce higher quality domain colorings. The new color schemes specifically enhance the display of singularities, symmetries and path integrals, and give better qualitative measures of the complex map.
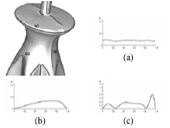
We propose a method to identify planar regions in volume data using a specialized version of the discrete Radon transform operating on a structured or unstructured grid. The algorithm uses an efficient discretization scheme for the parameter space to obtain a running time of O(N(T log T)), where T is the number of cells and N is the number of plane normals in the discretized parameter space. We apply our algorithm in an industrial setting and perform experiments with real-world data generated by topology optimization algorithms, where the planar regions represent portions of a mechanical part that can be built using steel plate.
Ulrich Bauer and Konrad Polthier
in: CyberWorld 2007 Conference Proceedings, Workshop "New Advances in Shape Analysis and Geometric Modeling", IEEE 2007.
Felix Kälberer, Matthias Nieser, and Konrad Polthier
in: Computer Graphics Forum 26 (3), 2007, pp. 375-384.
Presented at Eurographics 2007.
Klaus Hildebrandt and Konrad Polthier
in: Symposium on Geometry Processing 2007, pp. 203-212.
Klaus Hildebrandt, Konrad Polthier, and Max Wardetzky
Geometria Dedicata 123 (2006), pp. 89-112.
Felix Kälberer, Konrad Polthier, Ulrich Reitebuch and Max Wardetzky
in: Computer Graphics Forum 24 (3), 2005, pp.469-478.
Presented at Eurographics 2005.
Carsten Lange and Konrad Polthier
in: Special Issue of CAGD 2005 (U. Reif Ed.) and ZIB-Preprint 05-16.
Klaus Hildebrandt, Konrad Polthier, and Max Wardetzky
in: Symposium on Geometry Processing 2005, M. Desbrun and H. Pottmann (Eds.).
Presented at SGP 2005.
Klaus Hildebrandt, Konrad Polthier, and Eike Preuss
Ninth International Conference on Computer Aided Design and Computer Graphics (CAD/CG 2005).
Klaus Hildebrandt and Konrad Polthier
in: Computer Graphics Forum, 23 (3), 2004, and ZIB Preprint, 04-25.
- Best Student Paper Award at Eurographics 2004 -
Konrad Polthier
in: Global Theory of Minimal Surfaces, Proc. of the Clay Mathematics Institute Summer School, D. Hoffman (Ed.), CMI/AMS, (2005).
In differential geometry the study of smooth submanifolds with distinguished curvature properties has a long history and belongs to the central themes of this field. Modern work on smooth submanifolds, and on surfaces in particular, relies heavily on geometric and analytic machinery which has evolved over hundreds of years. However, non-smooth surfaces are also natural mathematical objects, even though there is less machinery available for studying them. Consider, for example, the pioneering work on polyhedral surfaces by the Russian school around Alexandrov [Aleksandrov/Zalgaller67Intrinsic], or Gromov's approach of doing geometry using only a set with a measure and a measurable distance function [Gromov99Metric]. Also in other fields, for example in computer graphics and scientific computing, we nowadays encounter a strong need for a discrete differential geometry of arbitrary meshes.
These tutorial notes introduce the theory and computation of discrete minimal surfaces which are characterized by variational properties, and are based on a part of the authors Habilitationsschrift [Polthier02Habilitationsschrift]. In Section we introduce simplicial surfaces and their function spaces. Laplace-Beltrami harmonic maps and the solution of the discrete Cauchy-Riemann equations are introduced on simplicial surfaces in Section . These maps are the basis for an iterative algorithm to compute discrete minimal and constant mean curvature surfaces which is discussed in Section . There we define the discrete mean curvature operator, derive the associate family of discrete minimal surfaces in terms of conforming and non-conforming triangles meshes, and present some recently discovered complete discrete surfaces, the family of discrete catenoids and helicoids.
Mirek Majewski and Konrad Polthier
in: Proc. of the 9th Asian Technology Conference in Mathematics, (2004), pp. 465-474
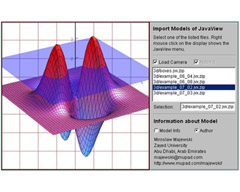
Mathematics education strongly benefits from the interactivity and advanced features of the Internet. The presentation of mathematical concepts on the Internet may go far beyond what we could demonstrate in traditional mathematics textbooks. In this paper we demonstrate, in a number of examples, the additional insight into complex mathematical concepts that can be gained from 3D interactive visualization embedded into web pages. Mathematical visualization is improving our teaching environments and the communication between teachers and students.
We combine two mathematical software systems—MuPAD as a development platform and JavaView for computation and online visualization of interactive mathematics experiments. We discuss the practical aspects of online publications and show some technical details about how to develop mathematical experiments on your own. The conference presentation will demonstrate MuPAD and JavaView components in live-action.
Steven P. Dugaro and Konrad Polthier
in: Algebra, Geometry, and Software Systems,
M. Joswig, N. Takayama (Eds) Springer Verlag (2003), pp. 255-275.
Konrad Polthier and Eike Preuß
in: Visualization and Mathematics III, Eds: H.C. Hege, K. Polthier,
Springer Verlag (2003), pp. 113-134.
Konrad Polthier
in: Nonlinear Partial Differential Equations, S. Hildebrandt and H. Karcher (Eds.) Springer Verlag (2002), pp. 127-143.
Konrad Polthier and Wayne Rossman
in: J. Reine und Angew. Math. (Crelle Journal), 549 (2002), 47-77.
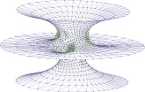
We define triangulated piecewise linear constant mean curvature surfaces using a variational characterization. These surfaces are critical for area amongst continuous piecewise linear variations which preserve the boundary conditions, the simplicial structures, and (in the nonminimal case) the volume to one side of the surfaces. We then find explicit formulas for complete examples, such as discrete minimal catenoids and helicoids.
We use these discrete surfaces to study the index of unstable minimal surfaces, by numerically evaluating the spectra of their Jacobi operators. Our numerical estimates confirm known results on the index of some smooth minimal surfaces, and provide additional information regarding their area-reducing variations. The approach here deviates from other numerical investigations in that we add geometric interpretation to the discrete surfaces.
Maria V. Andreeva, Ivan A. Dynnikov, and Konrad Polthier
in: Proc. of the International Congress on Mathematical Software, A. Cohen, X. Gao, N. Takayama (Eds.), World-Scientific (2002).
Konrad Polthier
in: Mathematics and Art, C. Bruter (Ed.), Springer Verlag (2002), pp.29-42.
Michael Joswig and Konrad Polthier
in: Multimedia Tools for Communicating Mathematics, Eds: J. Borwein, M. Morales, K. Polthier, J.F. Rodrigues, Springer Verlag (2002).
The archive Electronic Geometry Models is a new electronic journal for the publication of digital geometry models from a broad range of mathematical topics. The geometry models are distinguished constructions, counter examples, or results from elaborate computer experiments. Each submitted model has a self-contained textual description and is peer reviewed, and later reviewed by the Zentralblatt für Mathematik.
This paper gives in depth information about the principle ideas behind this service and discusses various technical issues. In particular, we show how XML related techniques are applied.
Color Plates: pic1.pdf, pic1.ps.zip, pic2.pdf, pic2.ps.zip)
Konrad Polthier, Samy Khadem, Eike Preuß, Ulrich Reitebuch
in: Multimedia Tools for Communicating Mathematics, Eds: J. Borwein, M. Morales, K. Polthier, J.F. Rodrigues, Springer Verlag (2002).
Konrad Polthier and Eike Preuß
in: Scientific Visualization, Springer Verlag (2000). Proc. of Eurographics Workshop on Scientific Visualization, Amsterdam 2000
Preprint No. 448 TU-Berlin, SFB 288, 2000.
Michael Joswig and Konrad Polthier
in: Newsletter of the European Mathematical Society (EMS), 2000.
The first collection of reviewed electronic geometry models is
available online at the new Internet server
http://www.eg-models.de.
This archive is open for any geometer to publish new geometric models,
or to browse this site for material to be used in education and research.
Access to the server is free of charge.
The geometry models in this archive cover a broad range of mathematical topics from geometry, topology, and, to some extent, from numerics. Examples are geometric surfaces, algebraic surfaces, topological knots, simplicial complexes, vector fields, curves on surfaces, convex polytopes, and, in some cases, experimental data from finite element simulations.
All models of this archive are reviewed by an international team of editors. The criteria for acceptance follow the basic rules of mathematical journals and are based on the formal correctness of the data set, the technical quality, and the mathematical relevance. This strict reviewing process ensures that users of the EG-Models archive obtain reliable and enduring geometry models. For example, the availability of certified geometry models allows for the validation of numerical experiments by third parties. All models are accompanied by a suitable mathematical description. The most important models will be reviewed by the Zentralblatt für Mathematik.
Michael Joswig and Konrad Polthier
in: Mitteilungen der Deutschen Mathematiker Vereinigung (DMV), 2000.
Konrad Polthier
in: M. Emmer (Ed) Mathematica e Cultura 3, Springer Verlag (2000), Preprint No. 447 TU-Berlin, SFB 288, 2000.
The future of mathematical communication is strongly related with the internet. On a number of examples, the present paper gives a futuristic outlook how mathematical visualization imbedded in the internet will provide new insight into complex phenomena, influence the international cooperation of researchers, and allow to create online hyperbooks combining interactive experiments and mathematical texts.
Using the software JavaView we discuss practical aspects of online publications and give technical details on the ease of implementations. The online version of this paper is a sample interactive document with visualization examples and numerical experiments.
Konrad Polthier, Markus Schmies
in: Data Visualization, Springer Verlag (1999). Proceedings of
Eurographics Workshop on Scientific Visualization, Vienna 1999
Preprint: TU-Berlin, SFB 288, Preprint No. 374, 1999.
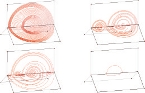
On a curved surface the front of a point wave evolves in concentric circles which start to overlap and branch after a certain time. This evolution is described by the geodesic flow and helps us to understand the geometry of surfaces.
In this paper we compute the evolution of distance circles on polyhedral surfaces and develop a method to visualize the set of circles, their overlapping, branching, and their temporal evolution simultaneously. We consider the evolution as an interfering wave on the surface, and extend isometric texture maps to efficiently handle the branching and overlapping of the wave.
Axel Friedrich, Konrad Polthier, Markus Schmies
in: Proc. of the 15th Spring Conference on Computer Graphics, Comenius University, Bratislava 1999, ISBN 80-223-1357-2, pp. 93--98.
View-dependent rendering allows interactive visualization of larger scenes. A well-known artifact is the popping problem in animations resulting from temporal differences in the level of detail between the view-dependent representations used in subsequent frames.
We solve the popping problem by computing view-dependent representations of a scene only at every n-th frame, and smoothly interpolate adjacent keyframe sections to obtain the representations for all in-between frames. Additionally, we accelerate rendering at only minor accuracy costs since interpolation is much faster than computing a view-dependent for each displayed frame.
We use scenes represented as triangle hierarchies and fulfilling a special constraint allowing for fast interpolation without remeshing. In contrast to other approaches our method naturally extends to animated scenes whose geometry and mesh may adaptively change in time.
Axel Friedrich, Konrad Polthier, Markus Schmies
in: Proceedings of IEEE Visualization '98, October 1998,
Eds: David Ebert, Holly Rushmeier, Hans Hagen
Preprint: TU-Berlin, SFB 288, Preprint No. 342, 1998.
We consider interpolation between keyframe hierarchies. We impose a set of weak constraints that allows smooth interpolation between two keyframe hierarchies in an animation or, more generally, allows the interpolation in an n-parameter family of hierarchies. We use hierarchical triangulations obtained by the Rivara element bisection algorithm and impose a weak compatibility constraint on the set of root elements of all keyframe hierarchies. We show that the introduced constraints are rather weak.
The strength of our approach is that the interpolation works in the class of conforming triangulations and simplifies the task of finding the intermediate hierarchy, which is the union of the two (, or more,) keyframe hierarchies involved in the interpolation process. This allows for an efficient generation of the intermediate connectivity and additionally ensures that the intermediate hierarchy is again a conforming hierarchy satisfying the same constraints.
Konrad Polthier, Markus Schmies
in: Mathematical Visualization, Ed: H.C. Hege, K. Polthier
Springer Verlag, 1998, ISBN 3-540-63991-8, Pages 391
Preprint: TU-Berlin, SFB 288, Preprint No. 327, 1998
Bernd Oberknapp and Konrad Polthier
in: Visualization and Mathematics, Ed: H.C. Hege, K. Polthier
Springer Verlag, 1997, ISBN 3-540-61269-6, Pages 386
Preprint: Univ. Bonn, SFB 256, Preprint No. 501, 1997
Karsten Große-Brauckmann, Konrad Polthier
in: Visualization and Mathematics, Ed: H.C. Hege, K. Polthier
Springer Verlag, 1997, ISBN 3-540-61269-6, Pages 386
Preprint: SFB 288, TU-Berlin, Preprint No. 211, 1996
Charles Gunn, Armin Ortmann, Ulrich Pinkall, Konrad Polthier, and Uwe Schwarz
in: Visualization and Mathematics, Ed: H.-C. Hege, K. Polthier
Springer Verlag, 1997, ISBN 3-540-61269-6, Pages 386
Preprint: SFB 288, TU-Berlin, Preprint No. 260, 1997
Laboratory equipment: Foundation software classes and function libraries
Configuration of specific experiment: Computational network composed of objects
Monitor and control: Object inspection; 2D and 3D viewers
Running the experiment: Animation objects
Recording the experiment: Archiving and scripting
Disseminating result: Documentation
Karsten Große-Brauckmann, Konrad Polthier
Experimental Mathematics, Vol 6 (2), 1997, Page 13-32, 18 Figures
Preprint: Univ. Bonn, SFB 256, Preprint No. 414, 1995
Hermann Karcher, Konrad Polthier
Phil. Trans. R. Soc. Lond. A (1996) 354, 2077-2104
Preprint: SFB 288, TU-Berlin, Preprint No. 194, 1996
(.pdf 761 KB, w/o Appendix .ps.gz 507 KB, Appendix .ps.gz 483 KB, abstract)
Bernd Oberknapp, Konrad Polthier
in: Modeling - Virtual Worlds - Distributed Graphics, Ed: D.W. Fellner, Page 25-36, 10 Figures
Infix Verlag, 1995, ISBN 3-929037-98-X, Pages 200
Preprint: Univ. Bonn, SFB 256, Report No. 16, 1995
Karsten Große-Brauckmann, Konrad Polthier
in Book: Elliptic and Parabolic Methods in Geometry, Eds: B. Chow, R. Gulliver, J. Sullivan, Pages 23-46, Figures 14, AK Peters, Wellesley, 1996, ISBN 1-56881-064-4, Pages 203
Preprint: TU-Berlin, SFB 288, Preprint No. 153, 1995
Konrad Polthier, Martin Rumpf
in: Visualization in Scientific Computing, Eds: M. Goebel, H. Mueller, B. Urban
Pages 137-153, Figures 5
Springer Verlag 1995, ISBN 3-211-82633-5, Pages 238
Preprint: Univ. Bonn, SFB 256, Report No. 13, 1994
Ulrich Pinkall, Konrad Polthier
Experimental Mathematics, Vol 2 (1), 1993, Page 15-36, 20 Figures
Preprint: TU-Berlin, SFB 288, Preprint No. 49, 1993
Konrad Polthier
in: Proceedings of the Center for Mathematics and its Application ANU Canberra, Vol 26, 1991, Workshop on 'Theoretical and Numerical Aspects of Geometric Variational Problems, Eds: G. Dziuk, G. Huisken, J. Hutchinson
Konrad Polthier
in: 'Geometric Analysis and Computer Graphics' Eds.: P. Concus, R. Finn, D. Hoffman, MSRI Bookseries 17, 1991, Springer and
Preprint: Univ. Bonn, SFB 256, Report No. 10, 1991
Konrad Polthier
Habilitationsschrift, TU-Berlin (Febr. 2002), 1-212.
Konrad Polthier
Bonner Mathematische Schriften, No. 263, 1994
Dissertation
Preprint: Univ. Bonn, SFB 256, Preprint No. 300, 1993
Konrad Polthier
in: ICIAM - Zurich Intelligencer, Springer-Verlag, 2007, pp. 42-43.
Konrad Polthier
Preprint No. 446, TU-Berlin, SFB 288, 2000
Ulrich Pinkall, Konrad Polthier
in: Spektrum d. Wissenschaft Sonderband 'Moderne Mathematik' (1996)
Gerd Faltings (Ed.)
T. Happe, K. Polthier , M. Rumpf, M. Wierse (1995)
in: Proceedings of the Workshop on 'Visualization - Dynamics and Complexity', Bremen, September 1995
Preprint: Math. Fak., Univ. Freiburg, Preprint No. 12 (1996)
Konrad Polthier
Spektrum der Wissenschaft, Dezember 1993 und
Tagungsband des Symposiums 'Simulation und Visualisierung' der IBM Bildungsgesellschaft, Mai 1994
Konrad Polthier, Martin Rumpf
Preprint: Univ. Bonn, SFB 256, Report No. 10, 1991
Hermann Karcher, Konrad Polthier
Spektrum der Wissenschaft, Oktober 1990