 See here for a video |
Prolog: Geodesic
Racing Track (Only in long version) The video prologue starts with a simulation of point waves on arbitrary surfaces. Particles in a wave front move along the straightest curves on a surface, so-called geodesic curves. The straightness property is visualized in the prologue by a motorcycle which drives along a geodesic. It has a fixed steering wheel and does not need to steer. The racing track is not curved for people who live on the surface. |
 |
Interfering Waves
and Branched Texture Maps Point waves on surfaces do overlap a number of times. This is in contrast to the euclidean case where a wave front would be always circular and have a linearly increasing diameter. A specific texture map technique was used to visualize the wave and especially the interference between overlapping parts of the wave. |
 See here for a video |
Introduction to
Geodesics Geodesic curves on surfaces are locally shortest curves. That means every small segment of a geodesic is the shortest connection between the end points of the segment. In contrast to straight lines in euclidean space there may exist a number of different geodesic curves connecting two given points on a surface. |
 See here for a video |
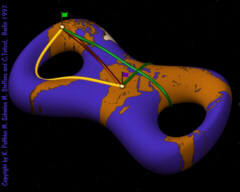
Special Phenomena
on Surfaces A point wave with origin on top of the torus will interfere at other parts of the surface. An additional effect seen on surfaces is the development of singularities, although the torus is a very smooth surface. This is a common phenomenon in the geometry of surfaces. The caustics of the wave front are the singularities of the differential of the exponential map. When using geodesics in numerical algorithms it is necessary to have a good understanding of the behavior of geodesics and such singularities. |
 See here for a video |
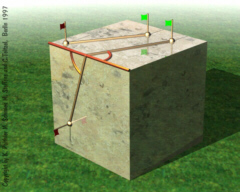
Geodesics on
Discrete Surfaces In numerics and visualization so-called discrete geometries are used and it is helpful to define discrete equivalents of terms from smooth differential geometry. Discrete geodesics on planar faces are just straight lines since the face is like a smooth planar surface. The definition of a geodesic across an edge is an immediate consequence since both faces can be made planar. |
 See here for a video |
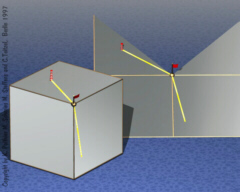
Straightest
Geodesics across Vertices More difficult is the definition of a discrete geodesic across a vertex of a discrete surface. Here the notion of discrete geodesic curvature is used and the arguments are of more technical nature. But the correspondence between geodesics and intrinsic light rays on surfaces provides a simple heuristic how a geodesic would surpass a vertex. It would bisect the total angle of the surface at a vertex. |
 See here for a video |
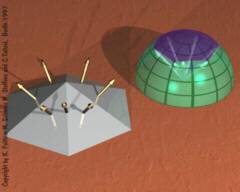
Discrete Surfaces
and the Gauß Curvature On discrete surfaces the curvature is located at the vertices and can be visualized by the Gauß image. Namely, take the normal vectors of the faces around a vertex and parallel translate them to the origin of a unit sphere. Then the vectors cover a certain patch on the unit sphere whose oriented area is called the discrete Gauß curvature of the polygonal vertex. It characterizes the intrinsic metric of the surface and is used in the definition of discrete geodesic curves. |
 See here for a video |
Point Waves on
Discrete Surfaces Point waves on discrete surfaces show similar phenomena as those on smooth surfaces. Here the singularities of the wave are located at the isolated vertices of the surface. A wave front branches there: the front from the right interferes with the front from the left, and, additionally, there is a new front generated at the vertex. |
 |
Outlook with
Application to Vector Fields The video finishes with an outlook at further applications of geodesics. The straight line property makes them a suitable concept also in numerical methods used for the integration of vector fields on surfaces. In the final animation an initial noise textures is transported along the integral curves of a height vector field. |